3 измененных файлов с 13 добавлено и 0 удалено
+ 0
- 0
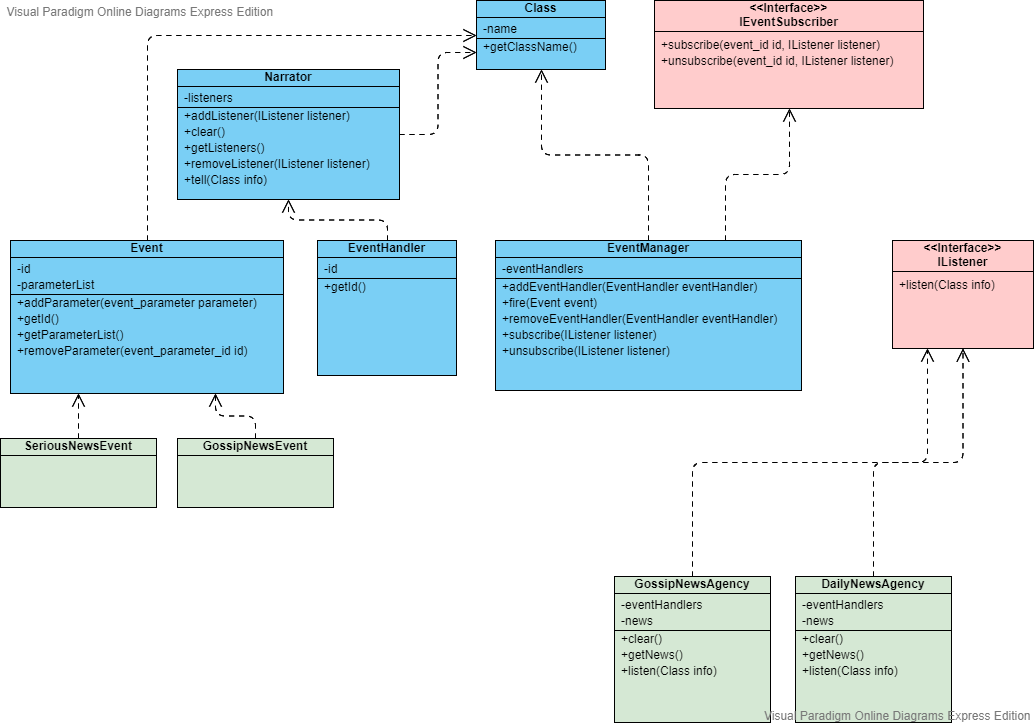
test/resources/event_handling_uml.png → doc/event_handling_uml.png
+ 13
- 0
doc/kv_file_definition.md
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
+ 0
- 0
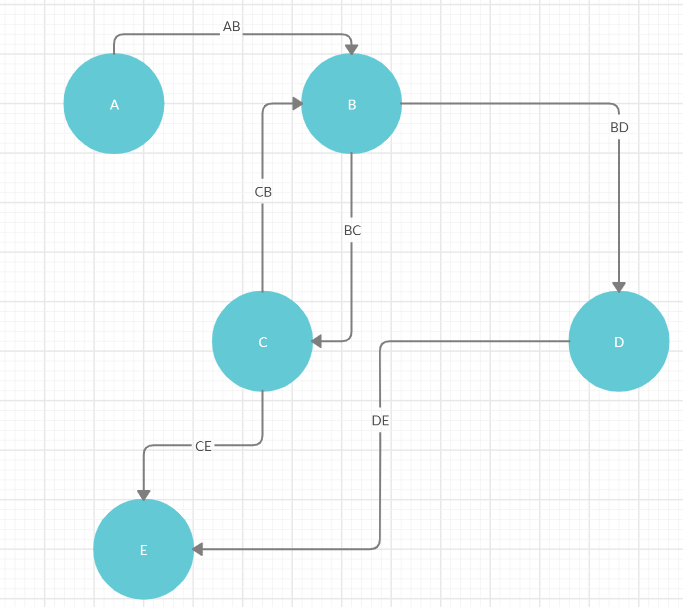
test/resources/state_machine_test.png → doc/state_machine_test.png